


: この文書について...
1=5
1 by -1
代数学 I No.5要約
 《剰余環、素イデアル、極大イデアル》
《剰余環、素イデアル、極大イデアル》
もちろん、体は必ず整域である。
これらの名前の由来はもっとあとのほうで述べる。
さしあたっては、次の例が重要である。
定義 5.3
素数
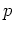
が与えられたとき、
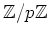
は(上の例に述べたように)元の数が
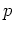
の体である。
この体を
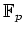
と書く。
(2)の例:
-
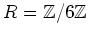 ,
, 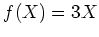 は一次式だが、
は一次式だが、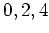 のどれを代入しても
0 である。
のどれを代入しても
0 である。
-
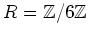 ,
,
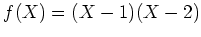 は二次式だが、
は二次式だが、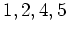 のどれを代入しても
0 である。
のどれを代入しても
0 である。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
- 正の数
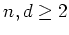 と、
と、
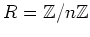 上の
上の 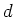 次多項式
次多項式 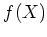 で、
で、
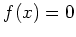 をみたす
をみたす 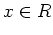 の数が
の数が 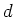 個より多いものの例を
挙げ、実際にそのような
個より多いものの例を
挙げ、実際にそのような 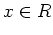 を
を 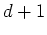 個以上書きなさい。
個以上書きなさい。
平成17年11月4日
![]() 《剰余環、素イデアル、極大イデアル》
《剰余環、素イデアル、極大イデアル》