


: この文書について...
代数学I要約 No.1
この講義の前半では、次の定理の証明を目標とする。
後半では、環や体の実例、とくに「一次元の環」
について詳しく扱う。
 《環の定義・部分環の定義》
《環の定義・部分環の定義》
環とは、足し算、引き算と掛け算ができる集合のことである。
部分環とは、部分集合であって環になっているもののことである。
定義 1.1 (環の定義)
集合
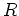
が環であるとは、足し算と呼ばれる写像
と掛け算と呼ばれる写像
が定義されていて次の性質を満たす時に言います。
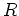 は足し算に関して可換群をなす。(
は足し算に関して可換群をなす。(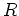 の足し算に関する単位元を
の足し算に関する単位元を
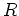 の零元といい、0 (時には
の零元といい、0 (時には 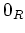 ) と書く。)
) と書く。)
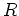 の積は結合法則を満たす。
の積は結合法則を満たす。
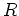 の足し算と掛け算は分配法則を満たす。すなわち、任意の
の足し算と掛け算は分配法則を満たす。すなわち、任意の
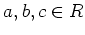 に対して、次のことが成り立つ。
に対して、次のことが成り立つ。
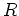 は積に関して単位元を持つ。すなわち、ある
は積に関して単位元を持つ。すなわち、ある 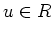 が存在して、
すべての
が存在して、
すべての 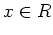 に対して、
に対して、
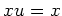 かつ
かつ 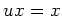 が成り立つ。
が成り立つ。
補題 1.1
環
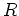
の単位元は、ただ一つである。
今後、環 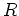 の単位元を
の単位元を 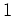 (時には
(時には 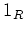 )と書く。
)と書く。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
問題 1.1
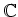
の部分環
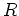
が
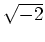
を含んだとします。
このとき、
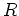
は
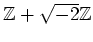
を部分集合として含むことを示しなさい。
問題 1.2
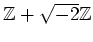
は
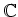
の部分環であることを示しなさい。
平成17年10月31日
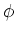 の像
の像
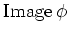 は
は 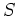 の部分環である。
の部分環である。
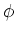 の核
の核
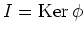 は
は 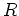 のイデアルである。
のイデアルである。
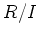 は
は
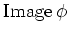 と同型である。
と同型である。
![]() 《環の定義・部分環の定義》
《環の定義・部分環の定義》
![]() の単位元を
の単位元を ![]() (時には
(時には ![]() )と書く。
)と書く。