


: この文書について...
代数学演習 I 問題 No.11

問題 11.1
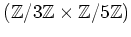
の元を全て挙げなさい。
問題 11.2
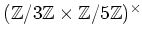
の元を全て挙げなさい。
問題 11.3
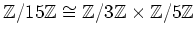
であることを示しなさい。
問題 11.4
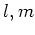
を互いに素な正の整数とし、
を
で決める。このとき、
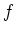 はうまく定義されていることを示しなさい。
はうまく定義されていることを示しなさい。
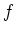 は環準同型であることを示しなさい。
は環準同型であることを示しなさい。
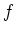 の核はどうなるか?
の核はどうなるか?
-
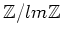 ,
,
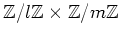 の元の個数をそれぞれ言いなさい。
の元の個数をそれぞれ言いなさい。
-
![$ f([x]_{lm})=([1]_l,[0]_m)$](img11.png) を満たす整数
を満たす整数 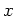 が
存在することを示しなさい。
が
存在することを示しなさい。
- 上の
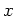 にたいして、
なる整数
にたいして、
なる整数 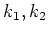 が存在することを示し、そのことから、
を満たす
が存在することを示し、そのことから、
を満たす 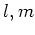 が存在することの証明を与えなさい。
が存在することの証明を与えなさい。
平成18年1月13日
![]()