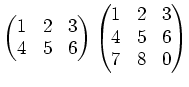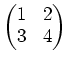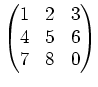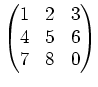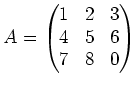: この文書について...
代数学演習 I 問題 No.5

問題 5.3
-
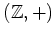 の部分群は全て
の部分群は全て
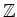 のイデアルであることを示しなさい。
のイデアルであることを示しなさい。
-
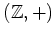 の部分群をすべて求めなさい。
の部分群をすべて求めなさい。
-
![$ ({\mathbb{C}}[X],+)$](img18.png) の部分群で、
の部分群で、
![$ {\mathbb{C}}[X]$](img11.png) のイデアルではないものの例を挙げなさい。
のイデアルではないものの例を挙げなさい。
問題 5.4
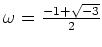
(
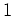
の三乗根)とします。この時、
は
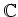
の部分環であることを示しなさい。
(記法に関する注意) この環は、
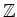
に、
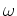
を付け加えた環になっている。
そこで、この環のことを、
![$ {\mbox{${\mathbb{Z}}$}}[\omega]$](img24.png)
とかく。
問題 5.5
-
![$ {\mbox{${\mathbb{Z}}$}}[\omega]$](img24.png) (前問参照) の単数群を求めなさい。
(前問参照) の単数群を求めなさい。
-
![% latex2html id marker 1160
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{3}]={\mbox{${\mathbb{Z}}$}}+{\mbox{${\mathbb{Z}}$}}\sqrt{3}$](img25.png) の単数群を求めなさい。
の単数群を求めなさい。
環 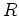 に対して、その元を成分にもつ行列を考えることができ、
通常の意味の和、差、積が(サイズがあっているという条件のもとで)
定義されて、一年生で習う線形代数のかなりの部分がそのまま
正しい。
に対して、その元を成分にもつ行列を考えることができ、
通常の意味の和、差、積が(サイズがあっているという条件のもとで)
定義されて、一年生で習う線形代数のかなりの部分がそのまま
正しい。
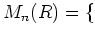
$R$ の元を成分にもつ $n×#times;n$ 行列
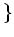
とおくと、これは(可換ではない)環である。
その単位元は 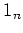 (
(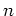 次の単位行列).
次の単位行列).
問題 5.7
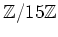
の元を成分にもつ行列の積
を計算し、できるだけ簡単な形、すなわち各成分の絶対値が
14以下の整数によって表されている形になるように直しなさい。
問題 5.8
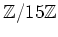
の元を要素にもつ行列
の逆行列を計算しなさい。
問題 5.9
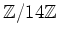
の元を要素にもつ行列
の逆行列を計算しなさい。
問題 5.10
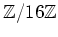
の元を要素にもつ行列
の逆行列を計算しなさい。
(今回の以下の問題では行列式やトレースの性質を自由に用いて良い。)
問題 5.11
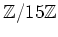
の元を要素にもつ行列
の逆行列は存在するだろうか。
理由を挙げて答えなさい。
(ヒント:
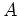
の逆行列
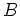
があったとする。
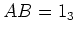
(3次の単位行列).
両辺の 行列式をとると...)
問題 5.12
どんな整数
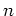
に対しても、
をみたす行列
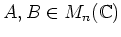
は存在しないことを示しなさい。
(ヒント:トレース)
問題 5.13
素数
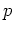
について、
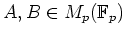
で、
を満たすものの例を挙げなさい。
(かなり難問である。
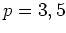
のときにまず試してみると良いかも知れない。)



: この文書について...
平成17年11月4日
![]()
![]() に対して、その元を成分にもつ行列を考えることができ、
通常の意味の和、差、積が(サイズがあっているという条件のもとで)
定義されて、一年生で習う線形代数のかなりの部分がそのまま
正しい。
に対して、その元を成分にもつ行列を考えることができ、
通常の意味の和、差、積が(サイズがあっているという条件のもとで)
定義されて、一年生で習う線形代数のかなりの部分がそのまま
正しい。