


: この文書について...
代数学III 要約 No.13
今日のテーマ

ガロアの基本定理を、詳細まで込めてもう一度書いておこう。
定理 13.1 (ガロアの基本定理)
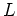
が
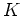
のガロア拡大のとき、
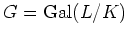
とおくと、
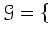
$G$ の部分群
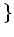
と
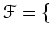
$L$ と $K$ の中間体
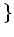
のあいだには一対一対応がつく。その対応は、
で与えられる。
さらに、
-
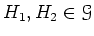 に対して、
に対して、
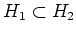 と
と
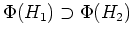 とは同値。
とは同値。
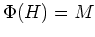 のとき、
のとき、
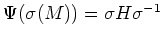 .
.
-
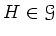 が
が 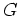 の正規部分群であることと、
の正規部分群であることと、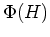 が
が
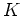 の正規拡大であることとは同値。
の正規拡大であることとは同値。
次のことは本筋というわけではないが本講義ではたびたび同様のことを
おこなってきたのでついでに述べておこう。
補題 13.1
体
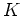
の元
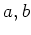
に対して、
ならば
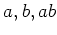
のうちどれか一つは
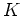
の元の二乗である。
問題 13.1
体
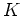
の元
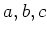
が、
![% latex2html id marker 715
$ [K(\sqrt{a},\sqrt{b},\sqrt{c}):K]<8$](img22.png)
をみたすならば、
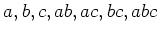
のうち
どれかは
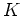
の元の二乗であることを示しなさい。
平成16年7月12日
![]()