


: この文書について...
代数学III 要約 No.8
今日のテーマ

を解こう。この方程式の根を
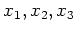 とする。
根が何であるか、具体的に知らないわけだが、その存在は既に知っている。
とする。
根が何であるか、具体的に知らないわけだが、その存在は既に知っている。
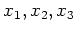 の持つ性質から逆算して、その解き方を見ようというわけだ。
の持つ性質から逆算して、その解き方を見ようというわけだ。
根と解の違いは何だろうか。解は方程式に代入してみたときの
答えである。
根は、もっと根本的なもので、
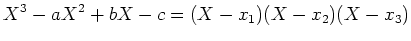 |
(★) |
と一次式の積に因数分解したときに現れるものをさす。
(したがって、当然、根がだぶる(重根)こともある。
「根」というときには厳密には多項式
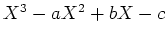 の根というのが正しい。)
の根というのが正しい。)
上の式(★)を展開することにより、いわゆる根と係数の関係
が得られる。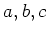 は知っている数だから、
は知っている数だから、
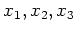 の
基本対称式の値を知っているということになる。前回に述べたことにより、
の
基本対称式の値を知っているということになる。前回に述べたことにより、
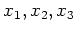 の対称式の値もこれらから(
の対称式の値もこれらから(
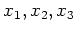 の値を個別に知らなくても)
計算できる。
の値を個別に知らなくても)
計算できる。
したがって、如何にして便利な対称式を作るか、が大事になる。ラグランジュの分解式
を考えてみよう。(ただし
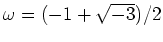 .)
これら自体は
.)
これら自体は
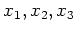 の対称式ではないが、
の対称式ではないが、
このことから、
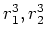 を二次方程式
の二根として計算することができて、
あとはその3乗根として
を二次方程式
の二根として計算することができて、
あとはその3乗根として 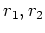 を計算できる。そこから
を計算できる。そこから
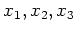 を
出すのは実は一次方程式を解けばよいので簡単である。
を
出すのは実は一次方程式を解けばよいので簡単である。
4次方程式の場合を考えよう。(前ページと記号が一部重複するが混乱しないこと)
根を
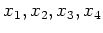 とおくと、
とおくと、
ここから根と係数の関係が得られ、やはり
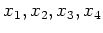 の
対称式は
の
対称式は 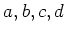 から(
から(
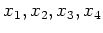 の値を知らなくても)
計算できる。
の値を知らなくても)
計算できる。
ラグランジュの分解式として、
をとる。
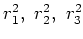 の基本対称式
の基本対称式
はそれぞれ
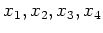 の対称式になっていることが分かり、したがって
の対称式になっていることが分かり、したがって 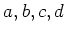 から計算できる。
すなわち、
から計算できる。
すなわち、
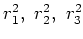 は
は
の三根であるから、前段のように巾根を用いて 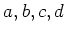 から計算できる。
あとはその平方根を計算すれば、
から計算できる。
あとはその平方根を計算すれば、
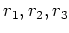 が計算されて、
一次方程式の根として
が計算されて、
一次方程式の根として
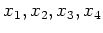 が計算されるという仕組である。
が計算されるという仕組である。
問題 8.1
三次方程式の解法(前ページ)で、
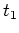
,
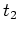
を
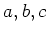
の多項式として実際に書き下しなさい。
(ヒント:
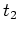
は直接やると難しいが、実は
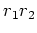
も
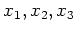
の対称式であることがわかるので、先ずそれを求めてそれから 3乗すればよい。)
問題 8.2
定数
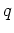
が与えられたとき、三次の多項式
の根を求める公式を作りなさい。
問題 8.3
四次方程式の解法で、
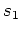
,
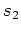
,
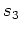
を
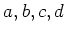
の多項式として実際に書き下しなさい。
(特に難問というほどではないが、計算はかなり面倒である。
可能ならば数式処理ソフトなどを活用するとよい。)
平成16年6月8日
![]()
![]() の根というのが正しい。)
の根というのが正しい。)
![]() とおくと、
とおくと、
![]() の対称式になっていることが分かり、したがって
の対称式になっていることが分かり、したがって ![]() から計算できる。
すなわち、
から計算できる。
すなわち、
![]() は
は