


: この文書について...
代数学II 要約 No.13
今日のテーマ

本講義では触れることができなかったが、有限アーベル群(=有限可換群)については、
次のことが知られている。
定理 13.1
有限アーベル群
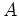
はかならず有限個の巡回群の直積と同型である。
この定理の証明はしないが、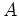 の各シロー群は必ず正規部分群であるから、
の各シロー群は必ず正規部分群であるから、
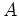 は必ずシロー群の直積に分解する。すなわち、
で、各
は必ずシロー群の直積に分解する。すなわち、
で、各 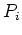 は素数
は素数 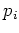 の巾
の巾 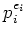 を位数に持つようなアーベル群である。
を位数に持つようなアーベル群である。
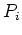 は
という形に書ける、というところが定理の主張である。
は
という形に書ける、というところが定理の主張である。
例 13.1
素数
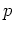
に対して位数
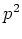
の群は必ずアーベル群である。
上の定理から、それは
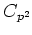
か、または
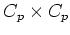
の
どちらかと同型であることが分かる。
今までに講義で出てきたことがらをうまく用いると、100以下程度の数 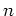 が
与えられたときに、位数
が
与えられたときに、位数 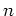 の群を求めることがかなり容易になる。
の群を求めることがかなり容易になる。
以下、そのやり方の例を幾つか挙げよう。
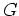 に正規部分群
に正規部分群 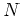 が存在することがわかると、
が存在することがわかると、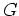 を調べるには
を調べるには 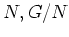 なる二つの群を先ず調べて、つぎにそれらから
なる二つの群を先ず調べて、つぎにそれらから 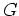 が
どのぐらい得られるか、という2ステップに分けられるので、
話がずいぶんやさしくなる。それに対して、
が
どのぐらい得られるか、という2ステップに分けられるので、
話がずいぶんやさしくなる。それに対して、
定義 13.1
群
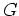
に
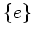
と
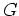
以外の正規部分群がないとき、
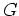
は
単純群と呼ばれる。
実は、位数 100 までの範囲では、素数位数の巡回群ではない単純群は
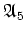 だけである。
次の問題は、
位数
だけである。
次の問題は、
位数 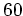 の単純群が
の単純群が
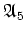 であることを証明するためのヒントである。
であることを証明するためのヒントである。
問題 13.1
位数
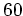
の群
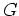
が単純群であると仮定するとき、
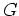
の
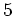
-シロー群の数
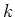
を求めよ。また、これにより
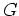
の
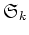
への群準同型
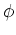
が得られるが、この
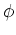
は単射だろうか。
理由を述べて答えなさい。
問題 13.2
位数
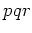
(
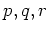
は素数、
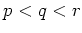
) の群
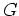
には正規部分群であるような
シロー群が少なくとも一つ存在することを示しなさい。
平成16年7月12日
![]()
![]() が
与えられたときに、位数
が
与えられたときに、位数 ![]() の群を求めることがかなり容易になる。
の群を求めることがかなり容易になる。
![]() に正規部分群
に正規部分群 ![]() が存在することがわかると、
が存在することがわかると、![]() を調べるには
を調べるには ![]() なる二つの群を先ず調べて、つぎにそれらから
なる二つの群を先ず調べて、つぎにそれらから ![]() が
どのぐらい得られるか、という2ステップに分けられるので、
話がずいぶんやさしくなる。それに対して、
が
どのぐらい得られるか、という2ステップに分けられるので、
話がずいぶんやさしくなる。それに対して、