今日のテーマ
![]()
今回は ![]() は奇素数の巾であるとする。
は奇素数の巾であるとする。
射影二次曲線の合同ゼータ関数を求めよう。![]() の二次式の斉次化を
考えるところからはじめても良いが、最初から二次斉次式を考える方が
楽なので、そうする。
の二次式の斉次化を
考えるところからはじめても良いが、最初から二次斉次式を考える方が
楽なので、そうする。
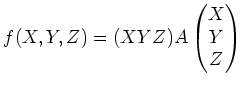
![]() の上基底をうまく取り換える(
の上基底をうまく取り換える(
![]() 座標変換をうまくとる)
ことにより、
座標変換をうまくとる)
ことにより、![]() の点を上手に求めることを考えよう。次の
(一見何でもない)命題が鍵になる。
の点を上手に求めることを考えよう。次の
(一見何でもない)命題が鍵になる。
![]() の基底を基本ベクトルから
の基底を基本ベクトルから
![]() に換えることにより
方程式は
に換えることにより
方程式は
この方程式の解の全体はすぐに書き下すことができて、
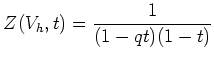
(今回はレポート問題はありません。来週は試験。)