


: この文書について...
代数学II要約 No.13
今日のテーマ:

(群 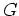 の表現)=(群環
の表現)=(群環
![$ {\mathbb{C}}[G]$](img3.png) の表現)
の表現)
中心
![$ Z({\mathbb{C}}[G])$](img4.png) は
は 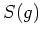 で生成される
で生成される
![$ {\mathbb{C}}[G]$](img3.png) の中心元はすべてある多項式をみたす。
の中心元はすべてある多項式をみたす。
表現は中心元の固有値で分解できる。
既約表現上では、中心元の作用は全て定数倍であらわされる。
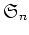 の表現はヤング図形から作ることができる。
の表現はヤング図形から作ることができる。
次のことは、講義では扱わなかったが、覚えておくと便利だろう。
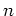 次のヤング図形
次のヤング図形 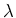 に対する
に対する
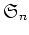 の表現
の表現
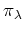 の表現空間
の表現空間 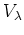 の基底として、
の基底として、
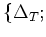
$T$ は $&lambda#lambda;$ を台とする標準盤
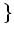
をとることができる。
ここで、標準盤とは、各行ごとに、番号が右の方に向かって増加し、
各列ごとに、番号が下の方に向かって増加しているような盤のことをいう。
試験問題予想例(レポートではない。)
完全に同じ問題は出ない。どこかしら数字や、群などがかわって出題される
だろう。
問題 13.1
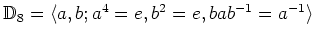
は
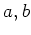
をそれぞれ
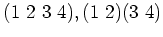
と同一視することにより
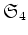
の部分群とみることができる。そこで、
![$ {\mathbb{C}}[\mathbb{D}_8]$](img17.png)
の中心の元
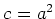
と、
4次のヤング図形
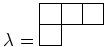
に対して、
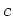
の
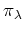
上での最小多項式を求めなさい。
問題 13.2
ある表現(ベクトル空間)
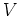
上に元
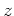
が(線型に)作用していて、
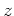
は
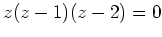
を満たしているとする。
このとき、
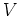
を
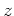
の固有空間(3つある)をそれぞれ
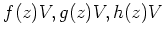
の形であらわせ。(具体的に
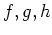
を求めよ。)
問題 13.3 (類題)
環
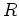
の元
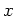
の最小多項式が
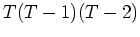
であるとき、
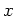
を用いて
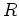
の巾等元を3つ作れ。
問題 13.4
次のような条件を同時に満足する正方行列
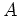
の例を挙げよ。(サイズは問わない)
-
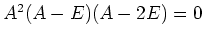
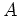 は非自明な3次の関係式を満足しない。
は非自明な3次の関係式を満足しない。
問題 13.5
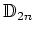
の群環
![$ {\mathbb{C}}[\mathbb{D}_{2n}]$](img32.png)
の中心の(
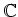
上の)次元を
求めよ。
平成15年7月23日
![]() の表現)=(群環
の表現)=(群環
![]() の表現)
の表現)
![]() は
は ![]() で生成される
で生成される
![]() の中心元はすべてある多項式をみたす。
の中心元はすべてある多項式をみたす。
![]() の表現はヤング図形から作ることができる。
の表現はヤング図形から作ることができる。
![]() 次のヤング図形
次のヤング図形 ![]() に対する
に対する
![]() の表現
の表現
![]() の表現空間
の表現空間 ![]() の基底として、
の基底として、