


: この文書について...
代数学II要約 No.2
今日のテーマ:

定義 2.1 (環の定義)
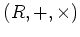
が環であるとは、集合
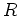
に足し算と呼ばれる写像
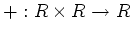
と掛け算と呼ばれる写像
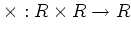
が定義されていて次の性質を満たす時に言う。
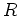 は足し算に関して可換群をなす。
は足し算に関して可換群をなす。
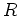 の積は結合法則を満たす。
の積は結合法則を満たす。
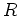 の足し算と掛け算は分配法則を満たす。
の足し算と掛け算は分配法則を満たす。
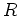 は積に関して単位元を持つ。
は積に関して単位元を持つ。
忘れた人は2回生の代数学の講義に戻るか、本講義の参考書
「加群十話」堀田良之著(朝倉書店)
などを参考にするとよい。
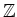 ,
,
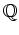 ,
,
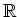 ,
,
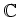 はそれぞれ環である。
一般に、環
はそれぞれ環である。
一般に、環 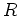 に対して、
に対して、
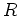 の元を成分にもつ
の元を成分にもつ 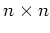 -行列全体のなす集合
-行列全体のなす集合 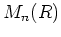 も環である。
も環である。
次のような例もある
例
環
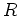
が与えられているとする。(例えば
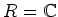
)
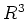
に次のような加法、乗法を定める。
このとき、
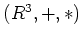
は環である。
問題 2.1
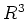
にベクトルの和
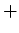
とベクトル積
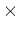
を
このとき、
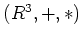
は環であるといえるだろうか。
いつでも上のような調子でかけ算を決めていたのではたまらない。実は
大抵の場合もっと分かりやすい積の定義があり得る。
上の例は実は 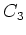 の群環と呼ばれるものと同じものになっている。
の群環と呼ばれるものと同じものになっている。
定義 2.2
有限群
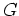
と、環
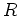
が与えられているとする。
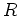
上の群環
![$ R[G]$](img21.png)
とは、
形式的な和の集合
に次のような和と積を導入したものである。
![$ R[G]$](img21.png) の乗法は、次のように言った方が洒落ているし、簡潔でもある。
の乗法は、次のように言った方が洒落ているし、簡潔でもある。
![$ R[G]$](img21.png) の乗法は、
の乗法は、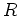 -双線形で、
-双線形で、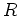 基底
基底 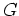 のそれぞれに対しては
その乗法は
のそれぞれに対しては
その乗法は 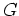 の乗法と一致する。
の乗法と一致する。
問題 2.2
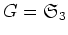
のとき、
![$ R[G]$](img21.png)
の積を例のような

の積として具体的に成分であらわしなさい。
2003/4/19
![]()
![]()
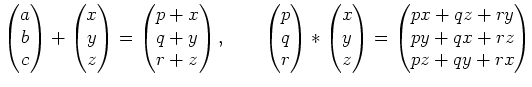
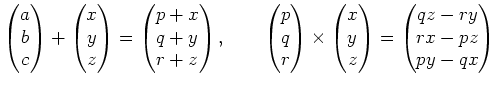
![]() の群環と呼ばれるものと同じものになっている。
の群環と呼ばれるものと同じものになっている。
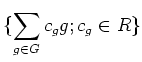
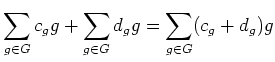
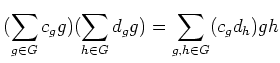
![]() の乗法は、次のように言った方が洒落ているし、簡潔でもある。
の乗法は、次のように言った方が洒落ているし、簡潔でもある。
![]() の乗法は、
の乗法は、![]() -双線形で、
-双線形で、![]() 基底
基底 ![]() のそれぞれに対しては
その乗法は
のそれぞれに対しては
その乗法は ![]() の乗法と一致する。
の乗法と一致する。