


: この文書について...
代数学特論II 要約 No.14
今日のテーマ:

関数環の定義の追加と復習。
定義 14.1
![$ {\mathbb{C}}[x]$](img2.png)
は
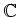
に
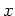
を追加してできる環、すなわち
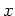
についての
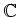
係数の多項式全体のなす環、
![$ {\mathbb{C}}[[x]]$](img5.png)
は
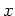
の形式的べき級数のなす環であった。
![$ {\mathbb{C}}[[x]]$](img5.png)
の部分環
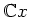
を、
![$\displaystyle {\mathbb{C}}\convergent{x}=\{f=\sum_{i=0}^\infty a_i x^i\in {\mathbb{C}}[[x]];$](img7.png)
$f$ の収束半径は正
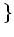
で定義し、
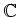
上の収束べき級数環と呼ぶ。。
インデックスの記号は、関数環
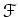 を明示して次のように書いておく
のがよい。
を明示して次のように書いておく
のがよい。
定義 14.2 (定義13.2再掲)
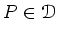
とする。
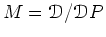
とおいて、
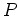
の
上のインデックスを
で定義する。(但し二つの次元がともに有限次元のとき。)
本講義の参考書「加群十話」にはマルグランジュの定理(161ページの定理10.1)が
書いてある。
定理 14.1 (マルグランジュ)
![$ P\in \mathcal D={\mathbb{C}}[x,\partial_x]$](img14.png)
を
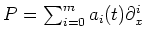
と書いたとき、
-
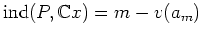
-
![% latex2html id marker 838
$ \operatorname{ind}(P,{\mathbb{C}}[[x]])=\underset {0\leq i \leq m}{\max}(i-v(a_i))$](img17.png)
(但し、
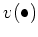
は
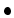
の零点の位数をあらわす。)
この講義ではこの定理の証明は述べないが、
次の例についてインデックスがどうなっているか、
述べたい。
例 14.1
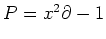
にたいして、
-
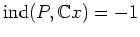
-
![$ \operatorname{ind}(P,{\mathbb{C}}[[x]])=0$](img22.png)
実際、この例については
と
はすぐにわかる。
がポイントで、これは微分方程式の形式的な解が必ずしも収束しないことと
対応している。
平成16年2月19日
![]()
![$\displaystyle {\mathbb{C}}\convergent{x}=\{f=\sum_{i=0}^\infty a_i x^i\in {\mathbb{C}}[[x]];$](img7.png) $f$ の収束半径は正
$f$ の収束半径は正 ![]() を明示して次のように書いておく
のがよい。
を明示して次のように書いておく
のがよい。