


: この文書について...
代数学特論II 要約 No.8
今日のテーマ:

例題 8.1 (ユークリッドの互除法)
等式
を満たす整数
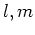
の組を一組求めよ。
(解答)
まず次のような計算を行なう
各々の行の行列算を組み合わせると、
を得る。この式の右辺に現れる正方行列はすべて
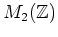 の元として
可逆であることに注意して、上の式を次のように変形することが出来る。
の元として
可逆であることに注意して、上の式を次のように変形することが出来る。
この式の第一行に着目すると、
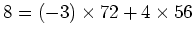 を得る。
を得る。
(答え)
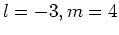 .
.
この手法は一変数多項式環でも同様に使える。
問題 8.1
![$ {\mathbb{C}}[X]$](img31.png)
の元
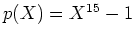
と
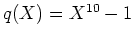
に対して、
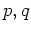
の最大公約数
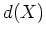
をもとめ、さらに
を満たす
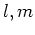
を求めよ。



: この文書について...
平成15年11月24日
![]()
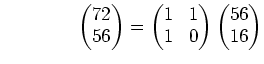
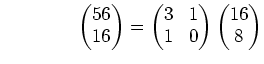
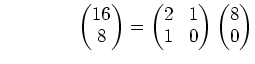
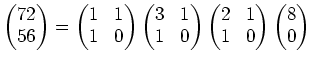
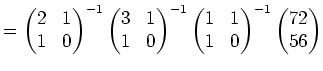
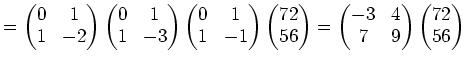
![]() .
.