代数学特論II 要約 No.1

今日のテーマ:

本講義は大まかに二部に分かれる。

• 行列のジョルダンの標準型と加群の理論
  • 弱固有空間への分解
  • 巾零行列の標準型
  • 応用

• 線型微分方程式の理論と加群の理論の関係
  • 微分作用素の因数分解による微分方程式の解法
  • 微分作用素のなす環の特質

今日は主に第一部の内容について述べることにしよう。

例えば、代数学II において、次のような状況が出てきた。

ある元 $z$ がある線型空間 $V$ に作用していて、$z^3-9z=0$ をみたせば、 $V$ は $z$ の固有値によって $3$ つの空間の直和に分解できる。

このようなことは、群の表現論だけではなくて、いろいろなところで現れる。 「元の作用」というのは行列で表現できるから、結局、 行列を一つ決めたときにそれによってどのように線型空間が分解されるのかが 問題になる。 代数学 II では、主に最小多項式が重根をもたないような元を扱ったが、 一般の行列はそのようなものばかりではない。最小多項式が 重根をもつ行列の扱いは若干注意が必要になる。これについても 若干解説する予定である。

さらに、行列をうまく用いると、「既存の体から、新しい体を作る」 ことができる。例えば、実数体 $\mbox{${\mathbb{R}}$}$ から ${\mathbb{C}}$ を作る一方法として、

$$\left\{ \begin{pmatrix} a & -b \\ b & a \end{pmatrix}; a,b \in \mbox{${\mathbb{R}}$} \right\}$$

を考えることがある。このやり方を応用するのである。 (実際には行列自体ではなくて、行列の満たす関係式のみから体を つくり出すこともできる。 これは可換体論では基本になる考え方である。ただしこの講義では行列を うまく用いて具体的に書くことにも力点をおく。)

問題 1.1  

$$\left\{ \begin{pmatrix} a & b \\ 2 b & a \end{pmatrix}; a,b \in \mbox{${\mathbb{Q}}$} \right\}$$

は体をなすことを示しなさい。

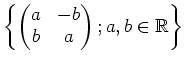
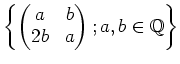
[各回の問題はレポートで提出すること。提出は特に指定しない限り 次回の講義の終了時間に行う(土基に直接渡す)ものとする。 複数の問題がある場合には、特に指定しない限りは 各回につき一問を解けばよい。

(介護等実習など、やむを得ない場合には その旨告げれば受け取ります。)]