代数学II 要約 No.14

試験の注意：

他人の迷惑になるものを除いては、何でも持ち込み可である。

電卓、コンピュータ等があったほうが簡単な問題も あり得るので、そのようなものを持ち込んでも構わない。

(今回の問題はレポート問題ではない。)

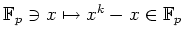
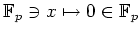
問題 14.1   写像 ${\mathbb{F}}_p \ni x \mapsto x^k-x \in {\mathbb{F}}_p$ は定値写像 ${\mathbb{F}}_p \ni x \mapsto 0 \in {\mathbb{F}}_p$ と等しいか、次の各々の場合に答えなさい。

1. $p=3,k=5$ のとき。
2. $p=5,k=5$ のとき。
3. $p=5,k=25$ のとき。
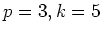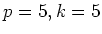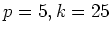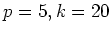4. $p=5,k=20$ のとき。

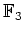
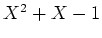
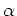
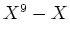
問題 14.2   ${\mathbb{F}}_3$ 上の多項式 $X^2+X-1$ の根を $\alpha$ とおく時、 ${\mathbb{F}}_{3}[\alpha]$ の多項式 $X^9-X$ を一次式の積に分解しなさい。

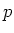
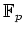
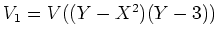
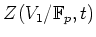
問題 14.3   奇素数 $p$ が与えられているとするとき、 ${\mathbb{F}}_p$ 上の方程式系 $V_1=V((Y-X^2)(Y-3))$ の 合同ゼータ関数 $Z(V_1/{\mathbb{F}}_p,t)$ を求めよ。

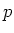
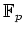
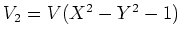
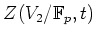
問題 14.4   奇素数 $p$ が与えられているとするとき、 ${\mathbb{F}}_p$ 上の2変数の方程式系 $V_2=V(X^2-Y^2-1)$ の合同ゼータ関数 $Z(V_2/{\mathbb{F}}_p,t)$ を求めよ。

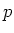
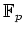
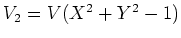
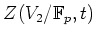
問題 14.5   奇素数 $p$ が与えられているとするとき、 ${\mathbb{F}}_p$ 上の2変数の方程式系 $V_2=V(X^2+Y^2-1)$ の合同ゼータ関数 $Z(V_2/{\mathbb{F}}_p,t)$ を求めよ。

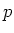
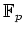
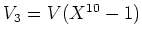
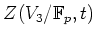
問題 14.6   奇素数 $p$ が与えられているとするとき、 ${\mathbb{F}}_p$ 上の1変数の方程式系 $V_3=V(X^{10}-1)$ の合同ゼータ関数 $Z(V_3/{\mathbb{F}}_p,t)$ を求めよ。