今日のテーマ:
![]()
前回、次の補題が残ってしまっていた。
一般に、ゼータ関数が ![]() によってどのように変わるかは複雑である。
例えば
によってどのように変わるかは複雑である。
例えば ![]() は各素数
は各素数 ![]() に対して
に対して
![]() 上の多項式と見られるが、
それが既約かどうかは
上の多項式と見られるが、
それが既約かどうかは ![]() によって異なる。
どのような
によって異なる。
どのような ![]() に対して既約であるかを判定するのに
便利なのが、平方剰余記号とその相互法則である。
相互法則の証明はいろいろ知られているが、この講義の話の応用として
有限体上のガウス和を用いた証明を紹介する。
に対して既約であるかを判定するのに
便利なのが、平方剰余記号とその相互法則である。
相互法則の証明はいろいろ知られているが、この講義の話の応用として
有限体上のガウス和を用いた証明を紹介する。
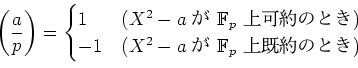
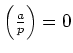 と定義する。
と定義する。
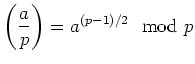
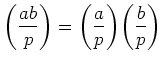
とくに
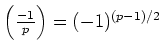 にも注意しておく。
にも注意しておく。
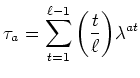
(なぜ、上の補題のような計算をしたくなるのか、 その一つのヒントはフーリエ級数論にある。)
上の補題を使うと次の定理を証明できる。但し(3)の証明は問題に譲る。
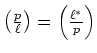 (但し
(但し
![]() の根を
の根を ![]() とするとき、
とするとき、
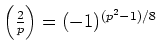 を示しなさい。
を示しなさい。