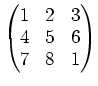: この文書について...
代数学II 要約 No.5
今日のテーマ:

諸君は線型代数と言うと
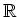 や
や 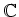 の上のそれしか知らないかも知れないが、
一般の体についても線型代数学の知識はほとんどそのまま使える。
例えば、行列, 行列式, 逆行列(ガウスの掃き出し法など),
線型空間とその基底、線型写像、などは体が違ってもほとんど
扱いは変わらない。
例えば問題5.1 を解いて感じをつかんで頂きたい。
の上のそれしか知らないかも知れないが、
一般の体についても線型代数学の知識はほとんどそのまま使える。
例えば、行列, 行列式, 逆行列(ガウスの掃き出し法など),
線型空間とその基底、線型写像、などは体が違ってもほとんど
扱いは変わらない。
例えば問題5.1 を解いて感じをつかんで頂きたい。
但し、行列の固有値などについて固有方程式を解く必要があるので、
その根の取り扱いについて知るまで待たなければならない。
また、ノルムの正値性などを使う部分(二次形式の理論など)は修正する必要があったり、
問題によっては体の差が大きく効いてくる場合もある。臨機応変に対応して頂きたい。
定義 5.1
体
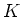
の部分集合
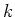
が
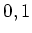
を含み、
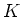
の演算をそのまま流用して
体になっている時、
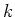
は
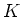
の部分体である(
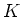
は
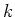
の拡大体である)と言う。
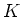
が
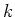
の拡大体ならば、
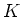
は
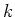
上の線型空間でもある。
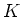
の
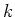
上の線型空間としての次元
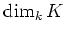
を
![$ [K:k]$](img8.png)
で書き表し、
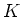
の
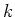
上の拡大次数と呼ぶ。(
![$ [K:k]$](img8.png)
は有限でない時もある。)
![$ [K:k]$](img8.png)
が有限である時、すなわち
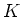
が
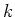
上の線型空間として
有限次元である時、
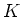
は
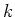
の有限次拡大であると言う。
補題 5.1
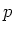
は
![$ k[X]$](img10.png)
の既約元であるとする。このとき、
![$ k[X]/(p(X)k[X])$](img11.png)
の
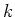
上の拡大次数は
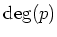
と等しい。
補題 5.2
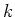
の拡大体
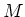
,
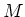
の拡大体
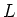
が与えられている時、
がなりたつ。
補題 5.3
有限体
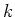
の拡大体
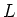
の
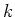
上の拡大次数が
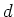
ならば、
がなりたつ。
とくに、
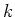
の標数を
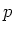
と書くと、
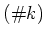
の元の個数は必ず
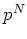
(
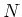
は正の整数)の形をしている。
(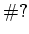 は
は 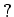 の元の数をあらわす記号である。)
の元の数をあらわす記号である。)
問題 5.1
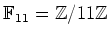
の元を成分に持つ行列
の行列式と逆行列とを求めなさい。
2002年5月22日
![]()
![]() や
や ![]() の上のそれしか知らないかも知れないが、
一般の体についても線型代数学の知識はほとんどそのまま使える。
例えば、行列, 行列式, 逆行列(ガウスの掃き出し法など),
線型空間とその基底、線型写像、などは体が違ってもほとんど
扱いは変わらない。
例えば問題5.1 を解いて感じをつかんで頂きたい。
の上のそれしか知らないかも知れないが、
一般の体についても線型代数学の知識はほとんどそのまま使える。
例えば、行列, 行列式, 逆行列(ガウスの掃き出し法など),
線型空間とその基底、線型写像、などは体が違ってもほとんど
扱いは変わらない。
例えば問題5.1 を解いて感じをつかんで頂きたい。