

: 置換行列
: その1:基本列ベクトル
: その1:基本列ベクトル
次のような (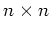 ) 正方行列はよくでてくる。
(つまり、主対角線の一つ上が、
) 正方行列はよくでてくる。
(つまり、主対角線の一つ上が、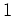 で、それ以外が 0.)
で、それ以外が 0.)
この行列については基本ベクトルの行き先をみるのが特に有効である。
列ベクトルを見ることにより、容易に次の関係を見ることができる。
つまり番号が一つづつずれるのである。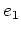 だけは例外で、これは 0 に写される。
(これを称して、
だけは例外で、これは 0 に写される。
(これを称して、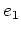 は
は 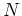 を施すと消されるとか、死ぬと
表現することがある。若干物騒な表現ではある。)
を施すと消されるとか、死ぬと
表現することがある。若干物騒な表現ではある。)
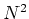 , つまり
, つまり 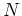 を2回施した結果はどうだろうか。
番号は2つづつずれて、
を2回施した結果はどうだろうか。
番号は2つづつずれて、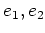 は 0 に写されることがわかるだろう。
つまり、
このことは、
は 0 に写されることがわかるだろう。
つまり、
このことは、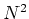 が次のような行列であらわされることを示している。
が次のような行列であらわされることを示している。
同様にして、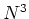 ,
,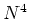 なども計算できる。
なども計算できる。
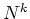 は基底を
は基底を 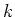 だけづらすことになるわけだ。(ただし、
だけづらすことになるわけだ。(ただし、
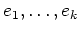 は
は
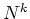 で消されることになる。)
で消されることになる。)
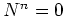 であることに、特に注意しよう。
であることに、特に注意しよう。
平成15年1月30日


![]() ,
,![]() なども計算できる。
なども計算できる。
![]() は基底を
は基底を ![]() だけづらすことになるわけだ。(ただし、
だけづらすことになるわけだ。(ただし、
![]() は
は
![]() で消されることになる。)
で消されることになる。)
![]() であることに、特に注意しよう。
であることに、特に注意しよう。