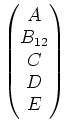
まあこのぐらいにしておこうか。ワルノリが好きな読者は更にいろいろと 検討してみるとよい。
調べる栄養は
まあこれもこの程度にしておこう。
前小節までに言ったように投入するものに対してこれらの栄養は近似的に 線型写像で表現できる。(いわゆる単純計算と言うやつである。)
ところで、例えばビタミンA ならビタミンA のトータルの量 は、少し粗く見ると(肉のビタミンA)+(野菜のビタミンA)+(その他のもののビタミンA) という風に計算できる。 ほかのビタミン、ミネラル、アミノ酸にも同じような個とがいえるのであって、 行列算はそのような意味である種の「ブロック」に分けることができる。
他方で、ビタミンを総じて考えるというのは「ビタミンベクトル」
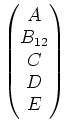
このような計算法がいわゆる行列のブロック区分けであって、 それは「ベクトル空間の直和」と密接に関係していることが 見てとれるだろう。
つまり、この例の場合は、
(材料空間)=(肉空間)+(野菜空間)+(その他のもの空間)
(栄養空間)=(ビタミン空間)+(ミネラル空間)+(アミノ酸空間)
なる空間の直和分解があって、 それに応じて行列算も分解できるというわけである。
余りクドクド書くと却って面倒なので、 あとは読者自らいろいろ考えて欲しい。