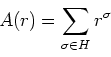Next: About this document ...
代数学特論 II 要約 No.11
今日のテーマ:
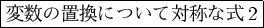 今回は前回積み残した補題の証明等について触れたいが、それだけでは芸が無いので
「平均」によって不変元を求める方法について書いておこう。
今回は前回積み残した補題の証明等について触れたいが、それだけでは芸が無いので
「平均」によって不変元を求める方法について書いておこう。
補題 11.1
群
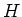
が環
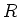
に作用しているとき、
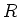
の任意の元
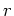
にたいして、
は
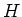
-不変な元になる。
この補題は 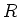 が有理数体を部分体として含むとき更に有用になる。
一般の環への一般の群の作用はここでは余り触れないが、
有理式の全体のなす体への置換群の作用の場合については理解していただきたい。
が有理数体を部分体として含むとき更に有用になる。
一般の環への一般の群の作用はここでは余り触れないが、
有理式の全体のなす体への置換群の作用の場合については理解していただきたい。
問題 11.1
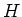
は、
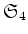
のなかで、
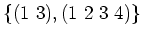
で生成される
部分群であるとする。このとき、
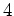
-変数有理関数体
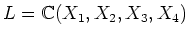
の
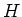
-不変元
で、
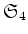
全体では不変ではないものの例を1つ挙げなさい。
2002-01-25
![]() 今回は前回積み残した補題の証明等について触れたいが、それだけでは芸が無いので
「平均」によって不変元を求める方法について書いておこう。
今回は前回積み残した補題の証明等について触れたいが、それだけでは芸が無いので
「平均」によって不変元を求める方法について書いておこう。