今日のテーマ:
![]()
前回次のことを示すことを残していた。
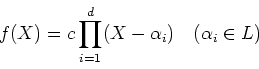
また、レポートで一変数の多項式の既約性の問題がでたので次のことを補足しておく。
では本題にうつる。次の例は二次拡大の様子をよく表している。
上の ![]() はもちろん
はもちろん ![]() の二次式
の二次式 ![]() の判別式である。
一般に、既約な代数的集合
の判別式である。
一般に、既約な代数的集合 ![]() と、その上の座標環
と、その上の座標環 ![]() の元
の元 ![]() をとったとき、
をとったとき、
![]() に
に
![]() を満たす元
を満たす元 ![]() を付け加えた体
を付け加えた体
![]() を考えることができて、その写像の様子も上の補題の
ように
を考えることができて、その写像の様子も上の補題の
ように ![]() から判断できる。ただし、既約性の問題は残る。
から判断できる。ただし、既約性の問題は残る。