


Next: About this document ...
代数学特論 II 要約 No.3
今日のテーマ:

既に注意したように、二つの体の間の準同型は必ず単射である。
したがって、体の間の準同型を調べる問題は、
体の間の「含む、含まれるの関係」(部分体と拡大体の関係)
を調べることに帰着される。
前者が成り立つ時、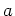 は
は 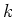 上代数的であると言い、後者が成り立つ時、
上代数的であると言い、後者が成り立つ時、
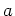 は
は 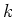 上超越的であると言われる。
上超越的であると言われる。
例 (超越元による単拡大の例)
- 1.
-
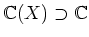
- 2.
-
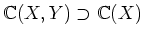
以下、体 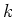 に対して、代数的集合と見たときの
に対して、代数的集合と見たときの 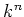 のことを
のことを
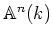 と書いて
と書いて 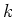 上の
上の 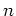 -次元アフィン空間と
よぶことにする。
-次元アフィン空間と
よぶことにする。
定義 3.1
一般に体
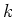
上の代数的集合
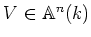
が既約であるとき
(これは代数IIで既にやったように
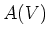
が整域であると仮定するのと同じである)、
A(V) の商体
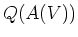
のことを
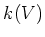
と書き、
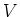
の (
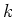
上の)関数体と呼ぶ。
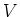 の関数体の代数的な元による単拡大は次のような具合になっている。
の関数体の代数的な元による単拡大は次のような具合になっている。
問題 3.1
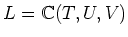
の部分体
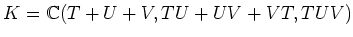
をとると、
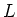
の元
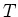
は
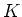
上代数的であることを、
を満たす
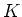
上の1変数多項式
![$f\in K[X]$](img42.png)
を具体的に与えることで示しなさい。
問題 3.2
上の
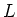
は
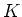
上単純拡大であることを示しなさい。(少し難問である。)
2001-10-26
![]()
![]() に対して、代数的集合と見たときの
に対して、代数的集合と見たときの ![]() のことを
のことを
![]() と書いて
と書いて ![]() 上の
上の ![]() -次元アフィン空間と
よぶことにする。
-次元アフィン空間と
よぶことにする。
![]() の関数体の代数的な元による単拡大は次のような具合になっている。
の関数体の代数的な元による単拡大は次のような具合になっている。