


Next: About this document ...
代数学特論 II 要約 No.1

体の理論の基本を、代数幾何的な見地から概説する。
代数学 II においては厳密性は少々落しても幾何学的直観が
身につくことを旨としていたが、こんどは少々細かいところまで
注意したい。
今日のテーマ:
写像 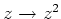 .
.
複素数体 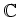 からそれ自身への写像
からそれ自身への写像
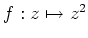 を考えよう。
前期の代数学IIでやったように、この写像には環準同型
を考えよう。
前期の代数学IIでやったように、この写像には環準同型
が対応している。
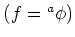 .
本講義では、この環準同型を
体
.
本講義では、この環準同型を
体
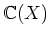 からそれ自身への準同型に拡張してその性質を見たいのであるが、
その前に
からそれ自身への準同型に拡張してその性質を見たいのであるが、
その前に 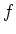 の性質についていくつか注意しておきたい。
の性質についていくつか注意しておきたい。
補題 1.1
- 1.
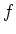 は 原点を原点に写す。
は 原点を原点に写す。
- 2.
- 原点以外では、
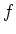 は2:1の写像である。
は2:1の写像である。
- 3.
- どんな連続写像
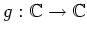 を持ってきても、
を持ってきても、
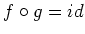 を満たすことは
不可能である。
を満たすことは
不可能である。
この補題の最後の主張は、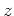 の平方根をとるということが意外に難しい
操作であることを示している。
の平方根をとるということが意外に難しい
操作であることを示している。
平方根、あるいはもっと一般に方程式の根、を詳しく調べるための
理論がいわゆるガロア理論である。
この講義でその全容を明らかにすることはできないが、いくつかの点については
解説する予定である。
問題 1.1
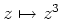
なる複素平面
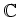
からそれ自身への写像を、
どの点がどのように移るかに注意しながら図示せよ。
(講義を受けたものは講義の
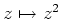
の図示を参考にすること。
不幸にして1回目の講義を欠席した場合には自分なりに工夫してみること。)
2001-10-02
![]()
![]() .
.
![]() からそれ自身への写像
からそれ自身への写像
![]() を考えよう。
前期の代数学IIでやったように、この写像には環準同型
を考えよう。
前期の代数学IIでやったように、この写像には環準同型