��������롣����ˡ�
��������롣���ΤȤ���
- 1.
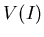 �Υ���դγ�����ʤ�����
�Υ���դγ�����ʤ�����
- 2.
-
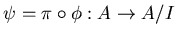 �γˤ���ʤ�����
������
�γˤ���ʤ�����
������
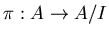 �ϼ����ʼͱ�
(
�ϼ����ʼͱ�
(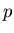 ���Ф��Ƥ��Υ��饹
���Ф��Ƥ��Υ��饹 ![$[p]$](img11.png) ���б��������Ʊ��)�Ǥ��롣
���б��������Ʊ��)�Ǥ��롣
- 3.
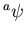 �����γ�����ʤ�����
�����γ�����ʤ�����
(����)
(1) ���η��ϱ����Ǥ��äơ��ߤǤϤʤ���
![\includegraphics[scale=0.5]{tube.ps}](img13.png)
(2)
![]() ��
��
![]() �η��������ܤ��ơ�¿�༰�Ȥ���
�η��������ܤ��ơ�¿�༰�Ȥ��� ![]() �� Ʊ�ͤˤ��ơ�¿�༰�Ȥ���
�� Ʊ�ͤˤ��ơ�¿�༰�Ȥ��� ![]() �����뤳�Ȥ��Ǥ�����������
�����뤳�Ȥ��Ǥ����������� ![]() .
���ʤ��
.
���ʤ��
![]() �������Ǥ���櫓����
�������Ǥ���櫓����
(3) �ֵ��Dz��٤��ä��褦�ˤ���ϱ߿��Ǥ��롣
![\includegraphics[scale=0.5]{cone.ps}](img34.png)
(����)
(1) ��ά���뤬���ֳʻҡפ����ʤ������������ʤ�Τ�Τˤʤ�ʤ��� �ְ㤤�ʤΤ˵��Ť����ߤ����� ľ��������ðǰ���ɤ�������ɤ��ΤǴ�ñ�ʤϤ��Ǥ��롣
(2)
����Ϥ䤵��������������ʪ���Ǥ��롣
![]() ��(2)��Ʊ���˽���ȡ����Τ褦�ʥ���դˤʤ롣
��(2)��Ʊ���˽���ȡ����Τ褦�ʥ���դˤʤ롣
![\includegraphics[scale=0.5]{parabora.ps}](img48.png)
(3)
![]() �Ȥ����ơ�
�Ȥ����ơ� ![]() �δط���
�δط��� ![]() ����
���� ![]() �δط�����
�������Ǹ��
�δط�����
�������Ǹ�� ![]() ��
�� ![]() ���֤�������Ф褤��
���ξ��Ϸ���Ū��
���֤�������Ф褤��
���ξ��Ϸ���Ū�� ![]() �Ȥ������˵դ˲뤫��ڤǤ��롣
������������Ū�ʷ������Ȥˤ�����12.1��(2)�β���ǽҤ٤��褦�ʥ����å���
���Ƥ����٤��Ǥ��롣
�Ȥ������˵դ˲뤫��ڤǤ��롣
������������Ū�ʷ������Ȥˤ�����12.1��(2)�β���ǽҤ٤��褦�ʥ����å���
���Ƥ����٤��Ǥ��롣
![]()
(4) ���Υ���դ�ֵ��ǽ����Ȥ����롣 �������äƾܤ��������Ͼ�ά���롣 (1)��(3)�Ȥ�Ʊ���˽ȡ� ���Τ褦�ˤʤ롣 �������Υ���դ���٤�Ȳ��������äƤ��뤫ʬ����䤹���������� ����դ���˽Ƥ����ơ� ������β����դ�Ҥä����֤�(������������Ҥ꤬ͤ�ä��)�� ���礦�ɤ��Τ褦�ʷ��ˤʤ롣�
![\includegraphics[scale=0.5]{singular.ps}](img55.png)