


Next: About this document ...
代数学 II 要約 No.12
今日のテーマ:
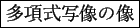
定義 12.1
代数的集合
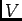
の座標環
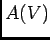
のイデアル
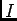
が与えられた時、
はやはり代数的集合である。これを (
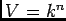
の時と同様に、)
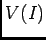
とかく。
補題 12.1
代数的集合
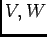
の間の多項式写像
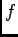
が与えられているとする。このとき、
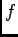
に対応する関数環の準同型写像(「引き戻し」)
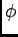
の核を
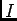
とおくと、
次のことが成り立つ。
- 1.
-
- 2.
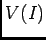 は
は
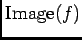 を部分集合として含む
を部分集合として含む 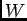 の代数的集合のうち、
最小のものである。
(Zariski 位相の言葉でいえばこれは
の代数的集合のうち、
最小のものである。
(Zariski 位相の言葉でいえばこれは 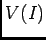 は
は
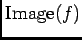 の(Zariski位相に関する)
閉包であると言ってもおなじことである。)
の(Zariski位相に関する)
閉包であると言ってもおなじことである。)
これまでのところを簡単な表にまとめると、次のような具合になる。
| 環論 |
代数幾何学 |
| 「モノ」の対応 |
多項式環
![$k[X_1,X_2,\dots,X_n]$](img14.png) |
n次元空間 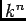 の座標環
の座標環 |
体 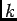 を含む環
を含む環 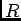 |
代数的集合 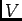 の座標環 A(V)
の座標環 A(V) |
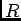 のイデアル
のイデアル 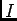 |
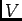 の代数的部分集合(Zariski 閉集合)
の代数的部分集合(Zariski 閉集合) 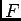 の
の |
| |
上で零になる関数全体 |
剰余環 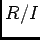 |
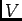 の代数的部分集合
の代数的部分集合 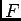 の座標環 A(F)
の座標環 A(F) |
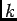 -準同型 -準同型
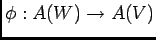 |
代数的集合の間の多項式写像
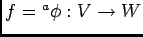 |
準同型の核
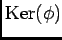 |
多項式写像の像の Zariski 閉包
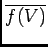 |
| 「性質」の対応 |
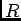 が非自明な巾零元を持つ
が非自明な巾零元を持つ |
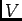 は二つの交わらない代数的集合和集合である
は二つの交わらない代数的集合和集合である |
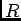 が非自明な零因子を持つ
が非自明な零因子を持つ |
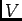 は可約な代数的集合
は可約な代数的集合 |
この表はかなり大まかなもので、厳密にはある程度の条件がないと左右の項目が
対応しなかったり、少しずつずれる場合もある。
それらの詳細についてはそれぞれの回の要約等を参照されたい。
一般的には、幾何的なイメージをうまく使って問題を把握し、そのあと
環論で正確な証明をつけるのがよいだろう。
問題 12.1
![$A=\mbox{${\Bbb R}$ }[X,Y,Z]$](img24.png)
から
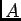
への環準同形写像
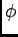
を
で定義する。さらに、
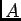
のイデアル
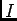
を、
で定義する。このとき、
- 1.
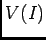 のグラフの概形を書きなさい。
のグラフの概形を書きなさい。
- 2.
-
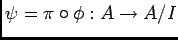 の核を求めなさい。
ただし
の核を求めなさい。
ただし
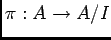 は自然な射影
(
は自然な射影
(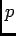 に対してそのクラス
に対してそのクラス ![$[p]$](img31.png) を対応させる準同型)である。
を対応させる準同型)である。
- 3.
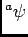 の像の概形を書きなさい。
の像の概形を書きなさい。
問題 12.2
![$B=\mbox{${\Bbb R}$ }[X,Y]$](img33.png)
から
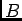
への環準同形写像
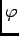
を
で定義する。さらに、
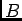
のイデアル
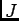
を、
で定義する。このとき、
- 1.
- 問題10.1 にならって
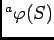 をグラフに書きなさい。
ただし、
をグラフに書きなさい。
ただし、
である。
- 2.
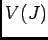 のグラフの概形を書きなさい。
のグラフの概形を書きなさい。
- 3.
-
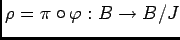 の核を求めなさい。
ただし
の核を求めなさい。
ただし
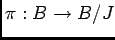 は自然な射影
(
は自然な射影
(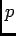 に対してそのクラス
に対してそのクラス ![$[p]$](img31.png) を対応させる準同型)である。
を対応させる準同型)である。
- 4.
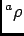 の像の概形を書きなさい。
の像の概形を書きなさい。
問題1, 2 ともに逆像のほうを計算してしまいがちなので注意。
グラフとよく見比べてみるといいだろう。
さらに、MuPAD などで実際にグラフを見てみるともっとよい。
MuPAD は高知大からなら
http://www.math.kochi-u.ac.jp/docky/kogi/
でダウンロードできる。



Next: About this document ...
2001-07-24
![]()