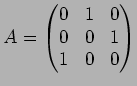 ,
,
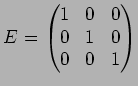 ,
,
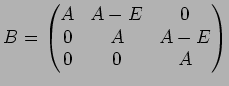 で定義し、さらに
で定義し、さらに
![]() とおく。
このとき、
とおく。
このとき、
- 1.
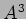 を求めなさい。
を求めなさい。
答え:
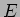 .
(これは単純計算であるが、
基本ベクトルの行き先 (
.
(これは単純計算であるが、
基本ベクトルの行き先 (
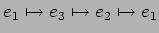 )を
見てやる方が若干早い。)
)を
見てやる方が若干早い。)
- 2.
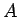 の固有値をすべて求めなさい。
の固有値をすべて求めなさい。
答え:
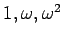 .
(これも簡単だろう。なお、上の 1.の結果から、
.
(これも簡単だろう。なお、上の 1.の結果から、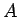 の固有値は必ず
3乗して
の固有値は必ず
3乗して 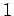 になることもわかっているはずである。)
になることもわかっているはずである。)
- 3.
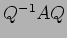 が対角行列であるような正則行列
が対角行列であるような正則行列 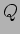 を一つ求めなさい。
を一つ求めなさい。
答え:
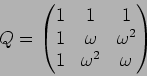
(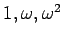 に対する固有ベクトルを求めて並べればよい。この場合には
に対する固有ベクトルを求めて並べればよい。この場合には
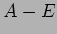 ,
,
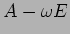 ,
,
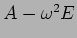 の核を求めるのが一番早いだろう。
ただし、この程度の行列なら基本ベクトルの行き先をよく見れば
慣れれば目のこで固有ベクトルがわかるはずである。
なお、
の核を求めるのが一番早いだろう。
ただし、この程度の行列なら基本ベクトルの行き先をよく見れば
慣れれば目のこで固有ベクトルがわかるはずである。
なお、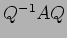 は
は
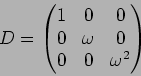
に等しい。)- 4.
- 上の
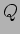 にたいし
にたいし
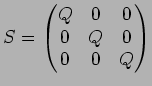 とおく。このとき
とおく。このとき 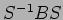 を求めなさい。
を求めなさい。
答え:
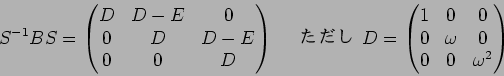
と書いてもいいし、ちゃんと成分で

と書いてもよい。また、次のようにブロックを意識した書き方でも構わない。
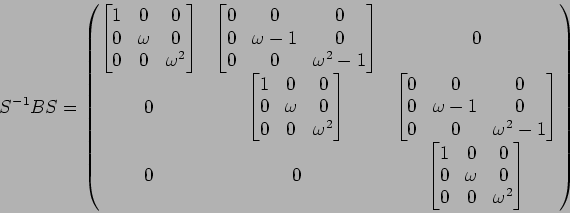
- 5.
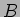 の固有値をすべて求めなさい。
の固有値をすべて求めなさい。
答え:
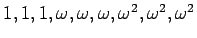 .
.
(
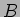 の固有方程式(固有値)と
の固有方程式(固有値)と 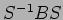 の固有方程式(固有値)はおなじ。)
の固有方程式(固有値)はおなじ。)
- 6.
-
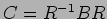 がジョルダンの標準型になるような
がジョルダンの標準型になるような 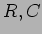 を求めなさい。
を求めなさい。
答え:
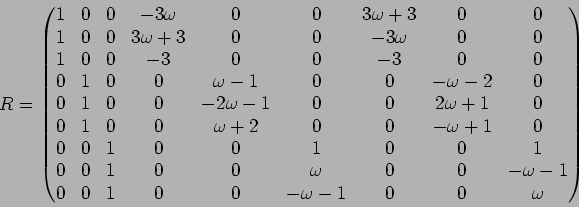
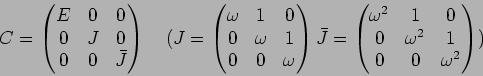
まず
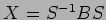 の列ベクトルに着目する。
の列ベクトルに着目する。
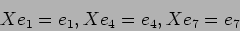
であるから、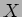 の固有値
の固有値 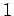 に対応する固有ベクトルとして
に対応する固有ベクトルとして
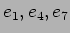 があることがわかる。同様にして、
があることがわかる。同様にして、
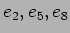 は
は 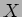 の固有値
の固有値 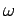 に対応する弱固有ベクトル,
に対応する弱固有ベクトル,
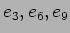 は
は 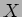 の固有値
の固有値 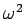 に対応する弱固有ベクトルであることがすぐにわかる。
このことに着目して、ひとまず
に対応する弱固有ベクトルであることがすぐにわかる。
このことに着目して、ひとまず 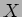 を次のように変換する。
を次のように変換する。
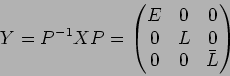
ただし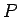 は次のような基底の置換に対応する行列である。
は次のような基底の置換に対応する行列である。
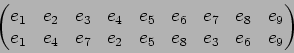
行列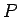 は
は
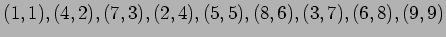 の各成分
が
の各成分
が 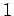 で残りは
で残りは 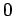 であるような行列である。
であるような行列である。
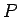 自体を書くのはばかばかしいのでここでは割愛する。
自体を書くのはばかばかしいのでここでは割愛する。
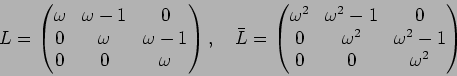
である。あとは
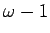 ,
,
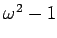 の部分を処理することだが、ここは単にベクトルを
何倍かすればよい。
の部分を処理することだが、ここは単にベクトルを
何倍かすればよい。
一応補題の形で述べておくとつぎのようになる。
補題 6.1(なお、行列のサイズをかえても同様のことをいうことができる。)
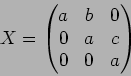
(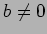 ,
,
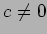 )
のジョルダンの標準型は
)
のジョルダンの標準型は
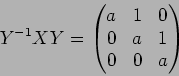
であたえられる。ここで、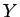 は
は
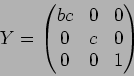
で与えられる行列である。 - 7.
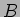 のジョルダン分解をしなさい。
のジョルダン分解をしなさい。
答え:
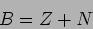
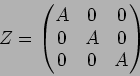

(これが
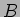 のジョルダン分解を与えることは、定理5.1 の1.-4. までの諸性質を
調べればよい。これはやさしい。定理5.1 の一意性の威力である。)
のジョルダン分解を与えることは、定理5.1 の1.-4. までの諸性質を
調べればよい。これはやさしい。定理5.1 の一意性の威力である。)
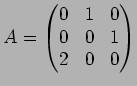 ,
,
![\begin{displaymath}Q=\begin{pmatrix}
1 & 1 & 1 \\
{\sqrt[3]{2}} & {\sqrt[3]{2}}...
...4}} & {\sqrt[3]{4}}\omega^2 & {\sqrt[3]{4}}\omega
\end{pmatrix}\end{displaymath}](img59.png)
![\begin{displaymath}S^{-1}BS
=
\begin{pmatrix}
D & D-E & 0 \\
0 & D & D-E \\
0 ...
...]{2}}\omega & 0 \\
0 & 0 & {\sqrt[3]{2}}\omega^2
\end{pmatrix}\end{displaymath}](img60.png)
![\begin{displaymath}\begin{pmatrix}
{\sqrt[3]{2}} & {\sqrt[3]{2}} -1 & 0 & 0 & 0 ...
...0 & 0 & 0 & 0 & 0 & 0 & {\sqrt[3]{2}} \omega^2\\
\end{pmatrix}\end{displaymath}](img63.png)
![\begin{displaymath}\begin{pmatrix}
-2{\sqrt[3]{2}} + {\sqrt[3]{4}} + 1 & 0 & 0 ...
...{4}} \omega^2
& 0 & 0 & {\sqrt[3]{4}} \omega
\\
\end{pmatrix}\end{displaymath}](img65.png)
![\begin{displaymath}\begin{pmatrix}
{\sqrt[3]{2}} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & ...
... & 0 & 0 & 0 & 0 & 0 & 0 & {\sqrt[3]{2}} \omega^2
\end{pmatrix}\end{displaymath}](img67.png)