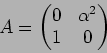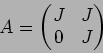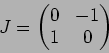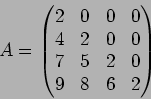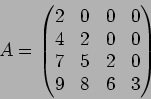今日のテーマ:
![]()
今回も、![]() といえば体を指すものとする。
といえば体を指すものとする。
上のような分解 ![]() を
を ![]() の ジョルダン分解(あるいは SN 分解)
と呼ぶ。
の ジョルダン分解(あるいは SN 分解)
と呼ぶ。
なお、![]() の固有値が
の固有値が ![]() に属さなくても、
に属さなくても、
![]() の上に分離的な元ばかりなら、
の上に分離的な元ばかりなら、![]() のジョルダン分解の
存在を示すことができる。
のジョルダン分解の
存在を示すことができる。
証明は、ガロア群の作用で ![]() が不変であることに
注意すれば簡単である。
が不変であることに
注意すれば簡単である。
固有値が ![]() に属さないような行列に対してジョルダン標準型などを求めるには、
に属さないような行列に対してジョルダン標準型などを求めるには、
![]() の適当な拡大体を考えてやるのが楽だが、そうもいかない場合もある。
そういうときには、つぎのような補題を援用すると役に立つことがある。
の適当な拡大体を考えてやるのが楽だが、そうもいかない場合もある。
そういうときには、つぎのような補題を援用すると役に立つことがある。
つぎの各例について、体 ![]() と行列
と行列
![]() にたいし、
にたいし、
![]() の ジョルダン分解をしなさい。(つまり、
の ジョルダン分解をしなさい。(つまり、![]() を求めなさい。)
を求めなさい。)