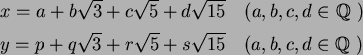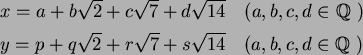Next: About this document ...
代数学 II 要約 No.7

定義 7.1 (定義6.3の再掲)
体
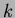
とその拡大体
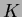
が与えられているとする。
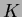
の
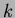
自己同型(あるいは、
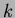
上の自己同型)とは、
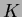
から
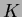
への同型
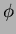
であって、
任意の
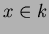
に対して
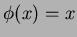
が成り立つものを言う。
定理 7.1
体
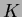
とその部分体
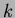
が与えられていて、
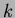
上の
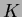
の自己同型
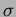
があったとする。このとき、
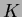
の任意の元
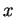
に対して、
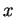
と
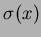
とは共役である。
この定理を元にして、与えられた体がどのくらい自己同型をもつか決定できる。
例 7.1
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img10.png)
の
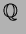
上の自己同型がどのくらいあるか求めてみよう。
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img10.png)
の
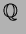
上の自己同型の一つを
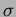
とすると、
上の定理により、
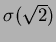
は
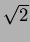
と
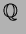
上
共役でなくてはならない。
そのことから、
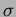
は次の二つのどちらかしかないことがわかる。
- 1.
-
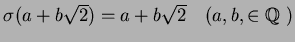 (恒等写像)
(恒等写像)
- 2.
-
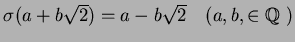
補題 7.1
体
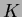
とその部分体
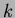
が与えられているとする。
このとき、
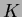
の
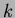
上の自己同型全体は(写像の同型に関して)群をなす。
定義 7.2
上の補題の群を
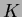
の
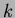
上の自己同型群といい、
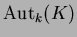
と書きあらわす。
補題 7.2
もし
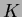
が
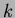
上環として
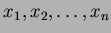
で生成されているならば、
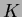
の
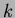
上の自己同型
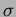
は

に
よって一意に決まる。
注意:上の補題で``環として''と書いた部分を``体として''に置き換えても
補題は成立する。証明の手間もほぼかわらない。
上の補題と、定理7.1 を用いると、体の自己同型がどのくらいあるか
だいたいわかる。
例 7.2
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt{2}])\cong{\mbox{${\Bbb Z}$ }}/2{\mbox{${\Bbb Z}$ }}.$](img19.png)
例 7.3
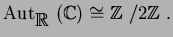
例 7.4
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt{2},\sqrt{5}])\...
... Z}$ }}/2{\mbox{${\Bbb Z}$ }}\times {\mbox{${\Bbb Z}$ }}/2{\mbox{${\Bbb Z}$ }}.$](img21.png)
例 7.5
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2}])=1.$](img22.png)
下の二例(および問題)では、
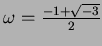 とおく。
とおく。
例 7.6
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])=\frak{S}_3$](img24.png)
(三次対称群).
例 7.7
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }[\omega]}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])={\mbox{${\Bbb Z}$ }}/3{\mbox{${\Bbb Z}$ }}$](img25.png)
(三次対称群).
上の例でも見られるように、自己同型の定義から次のことが成り立つことがわかる。
補題 7.3
三つの体
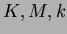
があって、
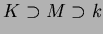
がなりたつとき、
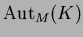
は
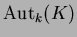
の部分群である。
今回は、問題7.1 は出席番号が奇数番号の人用、
問題7.2 は出席番号が偶数番号の人用とする。(7.3,7.4にはとくに制限は
ない。但しそれなりに難しい。)
問題 7.1
![$\mbox{${\Bbb Q}$ }[\sqrt{3},\sqrt{5}]$](img29.png)
の
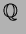
上の自己同型
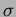
が、
を満たしたとする。このとき、
![$\mbox{${\Bbb Q}$ }[\sqrt{3},\sqrt{5}]$](img29.png)
の元
は
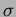
によってどのような元に写されるか(
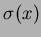
はいくらか)
述べよ。さらに、この
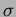
は実際に
をみたすことを、
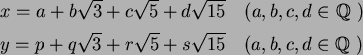
とおいて確かめてみよ。
問題 7.2
![$\mbox{${\Bbb Q}$ }[\sqrt{2},\sqrt{7}]$](img34.png)
の
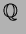
上の自己同型
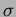
が、
を満たしたとする。このとき、
![$\mbox{${\Bbb Q}$ }[\sqrt{2},\sqrt{7}]$](img34.png)
の元
は
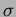
によってどのような元に写されるか(
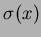
はいくらか)
述べよ。さらに、この
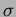
は実際に
をみたすことを、
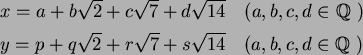
とおいて確かめてみよ。



Next: About this document ...
Yoshifumi Tsuchimoto
2000-06-05
![]()
![]() とおく。
とおく。