be the Jordan-Chevalley decomposition of
Let ![]() be the minimal polynomial of
be the minimal polynomial of ![]() .
If all of the roots of
.
If all of the roots of ![]() are separable over
are separable over ![]() ,
then
,
then ![]() and
and ![]() are defined over
are defined over ![]() .
(That means, they are matrices over
.
(That means, they are matrices over ![]() ).
).
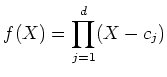
Let us define a polynomial
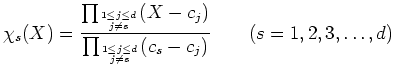
These polynomials are designed to satisfy the following property.
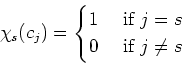
Then we further define
and
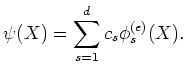
It is fairly easy to see that
holds.
The function ![]() is symmetric with respect to roots
is symmetric with respect to roots ![]() and
thus
and
thus ![]() is a polynomial with coefficients in
is a polynomial with coefficients in ![]() .
Thus
.
Thus ![]() (hence also
(hence also ![]() ) is defined over
) is defined over ![]() .
.
![]()
The following example shows that the ![]() -rationality of
-rationality of ![]() does
not necessarily hold when we drop off the assumption on
does
not necessarily hold when we drop off the assumption on ![]() .
.
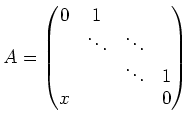
Then the minimal polynomial of
Thus the decomposition is not defined over