for some
for some
Since ![]() is projective and
is projective and ![]() is an integral domain,
is an integral domain, ![]() is torsion free.
So
is torsion free.
So
is injective. Since
Now, Let us paraphrase the condition that ![]() being projective.
First of all, the condition is equivalent to an existence of
being projective.
First of all, the condition is equivalent to an existence of ![]() -module
homomorphisms
-module
homomorphisms
such that
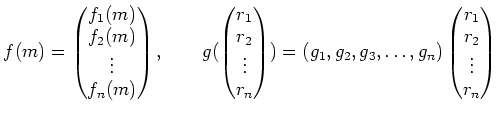
such that
Thirdly, each ![]() is represented by a linear map from
is represented by a linear map from ![]() to
to ![]() .
That means, by an element of
.
That means, by an element of ![]() .
.
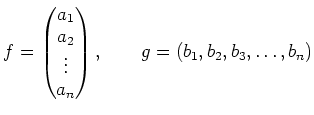
We may obtain several properties of
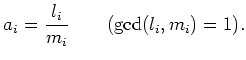
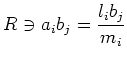
Since
By (iv) we see
By (v) we see
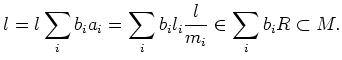
Thus
there exits an element
holds for any
Then by an argument similar to that in (I,Lemma 7.9), we see that
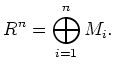
and that the multiplication by
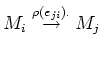
give isomorphisms between the modules. Hence we see easily that
and
We may easily see that