The treatment here essentially follows [1].
Let ![]() be a prime number.
Let
be a prime number.
Let ![]() be a (not necessarily commutative, but unital, associative) algebra
over
be a (not necessarily commutative, but unital, associative) algebra
over
![]() . We may also regard
. We may also regard ![]() as a Lie algebra over
as a Lie algebra over
![]() , the
bracket product being the ordinary commutator.
We would like to obtain a formula for
, the
bracket product being the ordinary commutator.
We would like to obtain a formula for
for
A first thing to do is to differentiate
the equation (1) by ![]() .
.
To compute the left hand side, we use a nice trick.
For any element ![]() , we denote by
, we denote by
![]() (respectively,
(respectively, ![]() )
an operator defined by
the left multiplication (respectively, the right multiplication) of
)
an operator defined by
the left multiplication (respectively, the right multiplication) of ![]() .
That is,
.
That is,
So from an ordinary result on commutative algebra, we have
We define
Then the equation above may be written as
Another interesting formula is the following.
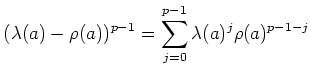
(To verify that it holds, we notice that for any commutative variable
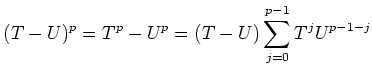
holds.) The above formula may then be rewritten as
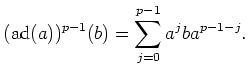
By suitable substitutions, we thus have
To sum up, we have obtained the following proposition.
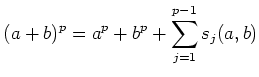
where
(Here,
An important corollary is the following.
holds for any
Then the map
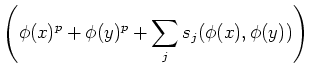 | ||
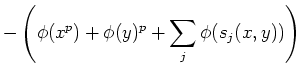 | ||
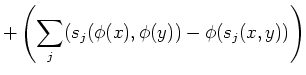 | ||