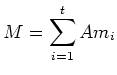
holds. If an ideal
then there exists an element
holds. If furthermore
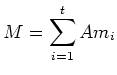
holds. If an ideal
then there exists an element
holds. If furthermore
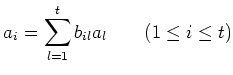
holds. In a matrix notation, this may be rewritten as
with
Now let
Then we have
On the other hand, since
![]()
Let us interpret the claim of the above theorem in terms of a sheaf
![]() on
on
![]() .
.
![]() is assumed to be finitely generated over
is assumed to be finitely generated over ![]() .
Note that this in particular means that every fiber of
.
Note that this in particular means that every fiber of
![]() on a
on a
![]() -valued point (for each field
-valued point (for each field ![]() ) is finite dimensional
) is finite dimensional ![]() -vector space.
In other words, it is ``a pretty little(=finite dimensional)
vector spaces in a row.''
-vector space.
In other words, it is ``a pretty little(=finite dimensional)
vector spaces in a row.''
The next assumption simply means that
![]() restricted to
restricted to ![]() is equal
to zero. So
is equal
to zero. So
![]() sits somewhere other than
sits somewhere other than ![]() .
.
The claim of the theorem (NAK) is that one may choose a regular function
![]() which ``distinguishes
which ``distinguishes ![]() and ``the support of
and ``the support of
![]() ''.
''.
![]() is equal to 0
on
is equal to 0
on ![]() and is equal to
and is equal to ![]() where
where
![]() sits.
sits.