

Next: ring homomorphism and spectrum
Up: (Usual) affine schemes
Previous: (Usual) affine schemes
Let 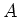 be a commutative ring. (Recall that we always assume ring to
be unital associative.)
Amazingly enough(!?), any element
be a commutative ring. (Recall that we always assume ring to
be unital associative.)
Amazingly enough(!?), any element 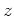 in
in 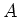 is central.
As we have seen in the Schur's Lemma, for any ``finite dimensional''
irreducible representation
is central.
As we have seen in the Schur's Lemma, for any ``finite dimensional''
irreducible representation 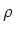 of
of 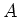 ,
, 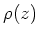 should be a
scalar. Thus we see that any irreducible ``finite dimensional''
irreducible representation of
should be a
scalar. Thus we see that any irreducible ``finite dimensional''
irreducible representation of
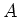 should be one dimensional.
Though this argument does not make sense when
should be one dimensional.
Though this argument does not make sense when 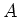 has no restriction
such as ``
has no restriction
such as ``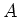 is finitely generated over a field'',
we may begin by considering a one-dimensional representation of
is finitely generated over a field'',
we may begin by considering a one-dimensional representation of 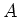 .
That means, a ring homomorphism
.
That means, a ring homomorphism
where 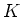 is a field.
One knows that
is a field.
One knows that
-
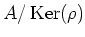 is an integral domain. That means, it has no
zero-divisor other than zero. (In this sense,
is an integral domain. That means, it has no
zero-divisor other than zero. (In this sense,
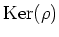 is said to
be a prime ideal of
is said to
be a prime ideal of 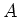 .)
.)
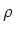 is decomposed in the following way.
is decomposed in the following way.
where 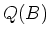 is the field of fractions of a ring
is the field of fractions of a ring 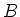 .
.
With a suitable definition of ``equivalence" of such representations,
we may identify equivalence class of representation with
the kernel
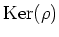 .
.
In other words, we are interested in prime ideals.
DEFINITION 1.1
Let
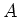
be a commutative ring.
Then we define the set
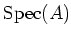
of spectrum of
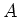
as the set of
prime ideals of
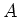
.
We note that for any
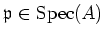 , we have a ring homomorphism
(``representation associated to
, we have a ring homomorphism
(``representation associated to
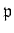 '')
'')
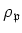 defined by
defined by
Since
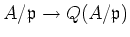 is an inclusion, we may say, by abuse of language,
that the value of an element
is an inclusion, we may say, by abuse of language,
that the value of an element 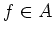 under the representation
under the representation
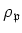 is equal to
is equal to
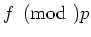 . We note further that
. We note further that
holds.
Let us now define a topology on
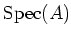 .
.
DEFINITION 1.2
Let
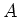
be a commutative ring.
For any
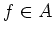
, we define a subset
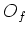
of
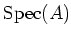
defined by
PROOF..
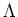
DEFINITION 1.4
The topology defined in the preceding Lemma is called the Zariski topology of
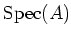
.
In Part II, we always equip
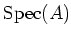 with the Zariski topology.
Thus for any commutative ring
with the Zariski topology.
Thus for any commutative ring 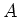 , we may always associate a topological
space
, we may always associate a topological
space
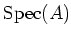 .
.


Next: ring homomorphism and spectrum
Up: (Usual) affine schemes
Previous: (Usual) affine schemes
2007-12-11
![]() .
.
![]() , we have a ring homomorphism
(``representation associated to
, we have a ring homomorphism
(``representation associated to
![]() '')
'')
![]() defined by
defined by
![]() .
.
![]() with the Zariski topology.
Thus for any commutative ring
with the Zariski topology.
Thus for any commutative ring ![]() , we may always associate a topological
space
, we may always associate a topological
space
![]() .
.