A crush course in quantum physics

Let us oversimplify the story and summarize the (earliest stage of) quantum physics in the following way. (For precise and physically more correct arguments, see for example [2])

1. A system is described by a Hilbert space $H$ .
2. Each physical quantity $A$ corresponds to an operator $O_A$ on $H$ .
3. A state corresponds to a vector $v\in H$ of length $1$ .
4. The expectation value $E_v(A)$ of $A$ when the system is in the state $v$ is given by
   $$E_v(A)=\langle v, O_A v \rangle \qquad ($$inner product$$)$$

(Note for mathematicians: when we use ``inner products'' in this Lecture, we usually mean a biadditive forms which are linear in the second variable and sesqui-linear in the first variable. That means,

$$\langle c_1 f,c_2 g \rangle=\overline{c_1} c_2 \langle f , g \rangle. \qquad (c_1,c_2\in \mathbb{C})$$

Please pay attention.)

One important example is a position $(q_1,q_2,q_3,\dots,q_n)$ and a momentum $(p_1,p_2,p_3,\dots, q_n)$ of a particle $P$ .

$$H=L^2(\mathbb{R}^n) ,\quad O_{q_j}=x_j, \quad O_{p_j}=i \partial/\partial x_j \qquad(j=1,2,3,\dots,n)$$

(Note for physicists: we employ a "system of units" such that the Planck's constant (divided by $2\pi$ ) $\hbar$ is equal to $1$ .)

Then the expectation of a function $f(x)\in C(\mathbb{R}^n)$ (say) when the state corresponds to a $L^2$ function $\phi\in H$ is given by

$$E_\phi(f)= \int \overline{\phi(x)} f(x) \phi(x) d x =\int f(x) \vert\phi(x)\vert^2 d x.$$

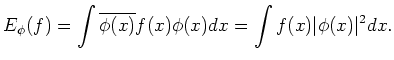
One may then regard $\vert\phi(x)\vert^2$ as a ``probability density'' of the particle $P$ on $\mathbb{R}^n$ . $\phi(x)$ is called the wave function of the particle. We should note:

1. $\phi(x)$ is complex valued. (It is not always positive nor real.)
2. the square of the absolute value of $\phi(x)$ (rather than $\phi(x)$ itself) is the probability.

In this sense, we sometimes use the term ``probability amplitude''. The square of the absolute value of the probability amplitude is the probability.

On the other hand, the expectation of a function $g(i \partial/\partial x)\in C(\mathbb{R}^n)$ should be:

$$E_\phi(g)=\int \overline{\phi(x)}g(i\partial/\partial x) \phi(x) d x.$$

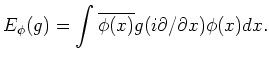
The computation becomes easier when we take a Fourier transform $F$ of $g$ .

$$\mathcal{F}[g](\xi)= (2 \pi)^{-n/2} \int f(x) e^{i x \xi} d x$$

or its inverse

$$\bar{\mathcal{F}}[g](\xi)= (2 \pi)^{-n/2} \int f(x) e^{-i x \xi} d x (=\mathcal{F}[g](-\xi)).$$

The Fourier transform is known to preserve the $L^2$ -inner product. That means,

$$\langle \mathcal{F}[g_1],\mathcal{F}[g_2]\rangle=\langle g_1,g_2\rangle$$

One of the most useful properties of the Fourier transform is that it transforms derivations into multiplication by coordinates. That means,

$$\mathcal {F}[(\partial/\partial x_j ) g] =i\xi_j \mathcal{F}[g].$$

Using the Fourier transform we compute as follows.

$$E_\phi(g)= \int \overline{\mathcal{F}[\phi]}g(-\xi) \mathcal{F}[\... ...al{F}[\phi]\vert^2 d x. =\int g(\xi) \vert\mathcal{\bar{F}}(\phi) \vert^2 d x.$$

We then realize that $\vert\bar{\mathcal{F}}[\phi] \vert^2$ plays the role of the probability density in this case.

Thus we come to conclude:

The probability amplitude of the momentum is the Fourier transform of the probability amplitude of the position.

The Fourier transform, then, is a way to know the behavior of quantum phenomena.

One may regard a table of Fourier transform (which appears for example in a text book of mathematics) as a vivid example of position and momentum amplitudes of a particle.

To illustrate the idea, let us know concentrate on the case where $n=1$ and assume that $\phi$ is a square root of the normal(=Gaussian) distribution $N(m,\sigma)$ of mean value $m$ and standard deviation $\sigma$ .

$$\phi(x)=\sqrt{N(m,\sigma)}= \sqrt{\frac{1}{\sqrt{2 \pi} \sigma}} e^{-\frac{(x-m)^2} {2 \cdot 2\sigma^2}}.$$

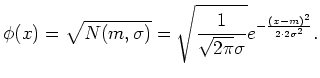
By using a formula

$$\mathcal{F}[e^{-x^2/a}]=\sqrt{\frac{a}{2}}e^{-a \xi^2/4},$$

we see that the Fourier transform of $\phi$ is given by

$$\mathcal{F}[\phi]=\sqrt{\frac{1}{\sqrt{2 \pi}\sigma^{-1}/\sqrt{2}... ... (\sigma^{-1}/\sqrt{2})^2} } =e^{i \xi m}\sqrt{N(0,\frac{1}{\sqrt{2}\sigma})},$$

so that the inverse Fourier transform is given as follows.

$$\bar{\mathcal{F}}[\phi] =e^{-i \xi m}\sqrt{N(0,\frac{1}{\sqrt{2}\sigma})}.$$

We observe that both $\vert\phi\vert^2$ and $\vert\bar{\mathcal{F}}[\phi] \vert^2$ are normal distribution, and that the standard deviation of them are inverse proportional to each other.

In easier terms, the narrower the $\vert\phi\vert^2$ distributes, the wider the transform $\vert\bar{\vert\mathcal{F}}\vert[\phi]\vert^2$ does.

It is a primitive form of the fact known as ``the uncertainty principle''.